Một sóng dừng trên một sợi dây đàn hồi có dạng $x=2A\sin \left( \frac{2\pi d}{\lambda } \right)\cos \left( \frac{2\pi }{T}t+\frac{\pi }{2} \right)$, trong đó u là li độ tại thời điểm t của phần tử M trên sợi dây mà vị trí cân bằng của nó cách gốc tọa độ O một đoạn x. Ở hình vẽ, đường mô tả hình dạng của sợi dây tại thời điểm t1 là đường (1). Tại các thời điểm ${{t}_{2}}={{t}_{1}}+\frac{3T}{8}$, ${{t}_{3}}={{t}_{1}}+\frac{7T}{8}$, ${{t}_{4}}={{t}_{1}}+\frac{3T}{2}$. Hình dạng của sợi dây lần lượt là các đường
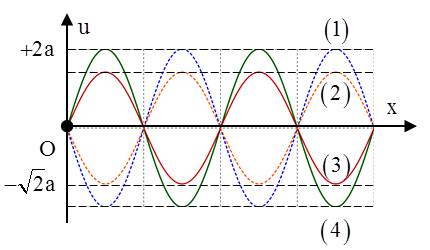
A. (3), (4), (2)
B. (3), (2), (4)
C. (2), (4), (3)
D. (2), (3), (4)
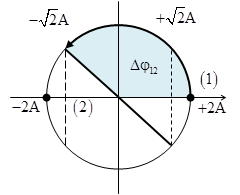
Tại thời điểm t$_{1}$, ta xét một phần tử tại bụng sóng. Các góc quét tương ứng với các thời điểm là
Bằng phương pháp đường tròn ta dễ dàng xác định được rằng tại thời điểm t$_{2}$, điểm khảo sát có li độ $u=-\sqrt{2}A$
Tương tự như vậy ta thứ tự của sợi dây là (3), (2) và (4)
Đáp án B