Năng lượng con lắc lò xo

Để giải những bài toán vật lý 12 ngoài phương pháp động lực học còn phương pháp khác là định luật bảo toàn năng lượng mà học sinh được học lớp 12. Ở đó học sinh đã biết đến năng lượng con lắc lò xo, thế năng đàn hồi và động năng. Với mong muốn giúp học sinh có thê công cụ giải bài này sẽ trình bày chi tiết từ những kiến thức căn bản nhất tới nâng cao. Mỗi công thức sẽ có một ví dụ giúp học sinh có thể vận dụng

1. Công thức năng lượng con lắc lò xo cần nhớ

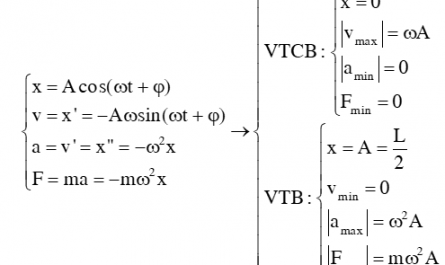
Giả sử người ta kích thích cho một con lắc lò xo dao động điều hòa với phương trình x = Acos(ωt + φ) thì

• biểu thức vận tốc con lắc v = – ωAsin(ωt + φ)
• biểu thức gia tốc con lắc a = – ω²x

Lúc này

• biểu thức thế năng đàn hồi: ${W_t} = \frac{1}{2}k{x^2} = \frac{1}{2}m{\omega ^2}{A^2}.{\cos ^2}\left( {\omega t + \varphi } \right)$
• Biểu thức động năng đàn hồi: ${W_d} = \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2}.{\sin ^2}\left( {\omega t + \varphi } \right)$
• Biểu thức cơ năng: $W = {W_d} + {W_t} = \frac{1}{2}k{x^2} + \frac{1}{2}m{v^2} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}k{A^2} = \frac{1}{2}mv_{\max }^2$

2. Ví dụ minh họa

Ví dụ 1: Một con lắc lò xo gồm vật nặng m = 200 g, dao đang dao động điêu hòa theo phương trình x = 2cos(πt + π/3) cm. Hãy xác định

a) biểu thức thế năng đàn hồi?

b) biểu thức động năng?

c) khi x = 1 cm thì động năng và thế năng vật là bao nhiêu?

Hướng dẫn giải

Theo đề bài:

• khối lượng vật nặng m = 200 g = 0,2 kg
• x = 2cos(πt + π/3) cm = 0,02cos(πt + π/3) m
• Tần số góc ω = π (rad/s)

Cơ năng của con lắc là ${\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,2.{\pi ^2}.0,{02^2} = {4.10^{ – 4}}\left( J \right)$

Mặt khác: $\omega = \sqrt {\frac{k}{m}} \Rightarrow k = m{\omega ^2} = 0,2.{\pi ^2} = 2\left( {\frac{N}{m}} \right)$

a) Biểu thức thế năng đàn hồi ${W_t} = {\rm{W}}.{\cos ^2}\left( {\omega t + \varphi } \right) = {4.10^{ – 4}}.co{s^2}\left( {\pi t + \frac{\pi }{3}} \right)\left( J \right)$

b) Biểu thức động năng đàn hồi ${W_d} = {\rm{W}}.si{n^2}\left( {\omega t + \varphi } \right) = {4.10^{ – 4}}.si{n^2}\left( {\pi t + \frac{\pi }{3}} \right)\left( J \right)$

c) khi x = 1 cm = 0,01 (m) thì thế năng đàn hồi ${{\rm{W}}_t} = \frac{1}{2}k{x^2} = \frac{1}{2}.2.0,{01^2} = {10^{ – 4}}\left( J \right)$

Lúc này động năng sẽ là ${{\rm{W}}_d} = {\rm{W}} – {W_t} = {4.10^{ – 4}} – {10^{ – 4}} = {3.10^{ – 4}}\left( J \right)$

Ví dụ 2: Người ta kích thích cho một vật nặng m = 100 g của con lắc lò xo dao động với biên độ 5 cm, biết chu kì dao động là 1 s. Hỏi Thế năng cực đại của con lắc lò xo bằng bao nhiêu?

Hướng dẫn giải

Theo đề:

• Khối lượng m = 100 g
• Biên độ A = 5 cm
• Chu kì T = 1 s

Tần số góc: $\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{1} = 2\pi \left( {\frac{{rad}}{s}} \right)$

Cơ năng của con lắc lò xo: ${\rm{W}} = \frac{1}{2}m{\omega ^2}{A^2} = \frac{1}{2}.0,1.{\left( {2\pi } \right)^2}.0,{05^2} = {5.10^{ – 3}}\left( J \right)$

Thế năng cực đại của con lắc lò xo bằng chính cơ năng: W_t = 5.10^-3 (J)

Ví dụ 3: Một con lắc lò xo dao động điều hòa với động năng cực đại là 0,2 J. Biết lò xo có độ cứng 25 N/m. Hỏi biên độ dao động của nó là bao nhiêu?

Hướng dẫn giải

Với dữ kiện đề bài:

• Động năng W_đmax = 0,2 J
• Độ cứng lò xo k = 25 N/m

Theo lý thuyết trên thì cơ năng chính bằng động năng cực đại W = W_đmax = 0,2 (J)

Khi đó: ${\rm{W}} = \frac{1}{2}k{A^2} \Leftrightarrow 0,2 = \frac{1}{2}.25.{A^2} \Leftrightarrow A = 0,127\left( m \right) = 12,7\left( {cm} \right)$

Những chia sẻ trên đây tạm kết thúc chủ đề năng lượng con lắc lò xo, hy vọng bài viết đã phần nào giải đáp được nhiều tắc mắc của các bạn. Mọi phản hồi chi tiết các bạn cứ để lại bình luận bên dưới hoặc gửi theo hòm thư tới admin. Những phúc đáp sẽ sớm được phản hồi trong ngày.