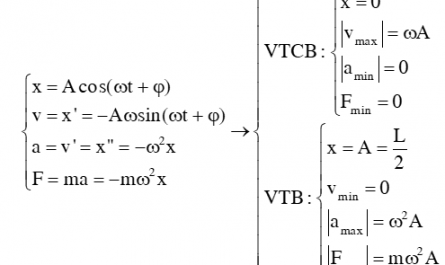
Năng lượng của mạch dao động LC lý tưởng

Năng lượng của mạch dao động là một chủ đề khá hay, nhờ công thức này ta có thể giải quyết được nhiều bài toán. Nếu bạn chưa nhớ được biểu thức cũng như những công thức quan trọng về năng lượng điện trường, năng lượng từ trường, năng lượng điện từ trường thì hãy xem bài viết dưới đây

1. Công thức năng lượng mạch dao động LC cần nhớ

Giả sử một mạch dao động lý tưởng LC có biểu thức điện tích q = Q₀cos(ωt + φ) thì

• cường độ dòng điện tức thời i = – ωQ₀sin(ωt + φ) = – I₀sin(ωt + φ) với I₀ = ωQ₀
• hiệu điện thế tức thời $u = \frac{q}{C} = \frac{{{Q_0}}}{C}.\cos \left( {\omega t + \varphi } \right)$

Khi đó năng lượng của mạch dao động LC

• Năng lượng điện trường ${{\rm{W}}_d} = \frac{1}{2}C{u^2} = \frac{1}{2}qu = \frac{{{q^2}}}{{2C}} = \frac{{q_0^2}}{{2C}}c{\rm{o}}{{\rm{s}}^2}(\omega t + \varphi )$
• Năng lượng từ trường ${{\rm{W}}_t} = \frac{1}{2}L{i^2} = \frac{{Q_0^2}}{{2C}}{\rm{si}}{{\rm{n}}^2}(\omega t + \varphi )$
• Năng lượng điện từ trường ${\rm{W}} = {{\rm{W}}_d} + {{\rm{W}}_t} = \frac{{Q_0^2}}{{2C}} = \frac{1}{2}LI_0^2$

2. Ví dụ vận dụng

Ví dụ 1: Một mạch dao động lý tưởng LC gồm cuộn cảm có hệ số L = 0,5 mH, tụ điện tích q = 5.10^-5sin(200πt) C.

a) Viết biểu thức năng lượng điện trường

b) Viết biểu thức năng lượng từ trường

c) Tìm năng lượng điện từ trường mạch dao động.

Hướng dẫn giải

Theo đề bài:

• Hệ số tự cảm L = 0,5 mH = 5.10^-4 (H)
• điện tích q = 5.10^-5sin(200πt) C = 5.10^-5cos(200πt – π/2) C

Từ biểu thức dòng điện ta suy ra cường độ dòng điện là i = – 200π.5.10^-5sin(200πt – π/2) A

a) Năng lượng điện trường được xác định theo công thức ${{\rm{W}}_d} = \frac{1}{2}\frac{{Q_0^2}}{C}.\cos \left( {\omega t + \varphi } \right)$

Ta thấy

• Điện tích cực đại Q₀ = 5.10^-5 (A)
• Diện dung tụ điện $\omega = \frac{1}{{\sqrt {LC} }} \Rightarrow C = \frac{1}{{{\omega ^2}L}} = \frac{1}{{{{\left( {200\pi } \right)}^2}{{.5.10}^{ – 4}}}} = {5.10^{ – 3}}\left( F \right)$

Khi đó: ${{\rm{W}}_d} = \frac{1}{2}\frac{{{{\left( {{{5.10}^{ – 5}}} \right)}^2}}}{{{{5.10}^{ – 3}}}}.\cos \left( {200\pi t – \frac{\pi }{2}} \right) = 2,{5.10^{ – 7}}.\cos \left( {200\pi t – \frac{\pi }{2}} \right)\left( J \right)$

b) Năng lượng từ trường ${{\rm{W}}_t} = \frac{1}{2}\frac{{Q_0^2}}{C}.\sin \left( {\omega t + \varphi } \right) = 2,{5.10^{ – 7}}.\sin \left( {200\pi t – \frac{\pi }{2}} \right)\left( J \right)$

c) Năng lượng điện từ của mạch dao động: W = W_t + W_đ = 2,5.10^-7 (J)

Ví dụ 2: Người ta ghép cuộn dây thuần cảm với một tụ điện có C = 6 µF, tạo thành một mạch dao động điện từ tự do. Dùng bộ nguồn để nạp cho tụ tới giá trị cực đại là 10 V.

a) Khi hiệu điện thế giữa hai đầu tụ điện là 2 V thì năng lượng điện trường? năng lượng từ trường bằng bao nhiêu?

b) Hãy xác định giá trị điện tích của tụ điện. Biết tại thời điểm này năng lượng điện trường bằng 3 lần năng lượng từ trường.

Hướng dẫn giải

Theo đề bài:

• C = 6 µF = 6.10^-6 (F)
• U₀ = 10 V

a) khi u = 2 V thì

• năng lượng điện trường giữa hai bản tụ điện: ${{\rm{W}}_d} = \frac{1}{2}C{u^2} = \frac{1}{2}.\left( {{{6.10}^{ – 6}}} \right){.2^2} = 1,{2.10^{ – 5}}\left( J \right)$
• năng lượng từ trường: ${\rm{W}} = \frac{1}{2}CU_0^2 = \frac{1}{2}.\left( {{{6.10}^{ – 6}}} \right){.10^2} = {3.10^{ – 4}}\left( J \right)$ => W_t = W – W_đ = 3.10^-4 – 1,2.10^-5 = 2,88.10^-4(J)

b) Ta có $\left\{ {\begin{array}{*{20}{l}} {{{\rm{W}}_d} = 3{W_t} \Rightarrow {W_t} = \frac{{{W_d}}}{3}}\\ {{\rm{W}} = {W_d} + {W_t}} \end{array}} \right. \Leftrightarrow {\rm{W}} = {W_d} + \frac{{{W_d}}}{3} \Leftrightarrow {W_d} = \frac{{3W}}{4}$

Khi thay số: $\frac{1}{2}.\frac{{{q^2}}}{{{{6.10}^{ – 6}}}} = \frac{3}{4}{.3.10^{ – 4}} \Leftrightarrow q = 5,{196.10^{ – 5}}\left( C \right)$

Điện tích của tụ cần tìm là q = 5,196.10^-5 (C)

Trên dây là những chia sẻ cơ bản nhất về năng lượng điện trường, năng lượng điện từ trường và năng lượng từ trường. Hy vọng bài viết này sẽ hữu ích với bạn.