Phương trình sóng dừng

Chủ đề phương trình là dạng toán nâng cao ứng với câu từ 8 điểm trở lên trong đề Vật lý chính thức của bộ giáo dục và đào tạo. Nó không chỉ đòi hỏi người học đào sâu kiến thức về sóng mà còn yêu cầu bạn phải có kiến thức toán học tương đối tốt.

Một lời khuyên là bạn nên xem kĩ lại các lý thuyết sóng dừng trước đây cũng như bài tập liên quan, như vậy bạn mới có thể học tốt bài này.

Giả sử tại nguồn sóng dao động với phương trình u = Acos(ωt) thì:

1. Phương trình sóng dừng có hai đầu cố định

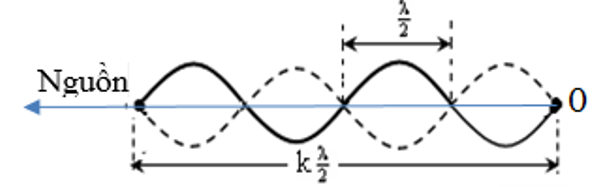
Phương trình có dạng: $u = 2a\sin \left( {\frac{{2\pi {x_1}}}{\lambda }} \right)\cos \left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right)\left( {cm} \right)$

Khi đó biểu thức biên độ có dạng: $A = \left| {2a\sin \left( {\frac{{2\pi {x_1}}}{\lambda }} \right)} \right|$

• ${A_{bụng}} = \left| {2a} \right| = {A_{\max }}$
• ${A_{nút}} = 0$
• $0 \le {A_M} \le 2a$

( với |x₁| là khoảng cách từ điểm khảo sát đến nút làm gốc).

Từ biểu thức biên độ ta thấy: $\frac{\omega }{{\frac{{2\pi }}{\lambda }}} = \frac{{\omega \lambda }}{{2\pi }} = \frac{{2\pi .f\lambda }}{{2\pi }} = f\lambda = v$ => Nếu biết được biểu thức truyền sóng thì ta suy ra được tốc độ truyền sóng ứng với sóng dừng có 2 đầu cố định.

2. Phương trình sóng dừng có 1 đầu cố định và 1 đầu tự do

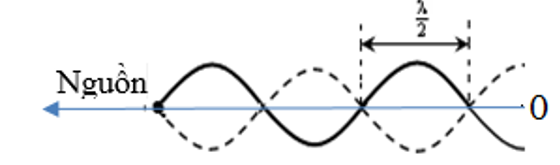
Phương trình dạng tổng quát: ${u_M} = 2a\cos \left( {\frac{{2\pi {x_2}}}{\lambda }} \right)\cos \left( {\frac{{2\pi }}{T}t + \frac{\pi }{2}} \right)\left( {cm} \right)$

Khi đó biểu thức biên độ có dạng: ${A_M} = \left| {2a\cos \left( {\frac{{2\pi {x_2}}}{\lambda }} \right)} \right|$

• ${A_{bụng}} = \left| {2a} \right| = {A_{\max }}$
• ${A_{nút}} = 0$
• $0 \le {A_M} \le 2a$

( với |x₂| là khoảng cách từ điểm khảo sát đến bụng làm gốc).

Bằng biến đổi tương tự, ta suy ra được sóng dừng với 1 đầu cố định và một đầu tự do: $v = \frac{\omega }{{\frac{{2\pi }}{\lambda }}}$

3. Bài tập

Ví dụ 1: Một sợi dây đàn hồi có sóng dừng có biểu thức $u = 3\cos \left( {\frac{{\pi x}}{5}} \right).\sin \left( {10\pi t – \frac{\pi }{6}} \right)\left( {cm} \right)$, trong đó ( x đo bằng cm, t đo bằng giây). Dựa vào biểu thức trên hay xác định tốc độ truyền sóng?

Hướng dẫn giải

Từ biểu thức biên độ: ${A_M} = \left| {3\cos \left( {\frac{{\pi x}}{5}} \right)} \right| \Rightarrow \frac{{2\pi }}{\lambda } = \frac{\pi }{5}$

Mặt khác: ω = 10π (rad/s)

Áp dụng công thức trên: $v = \frac{\omega }{{\frac{{2\pi }}{\lambda }}} = \frac{{10\pi }}{{\frac{\pi }{5}}} = 50\left( {cm/s} \right)$

Kết luận: Tốc độ truyền sóng là 50 cm/s.

Ví dụ 2. Tại một điểm M trên dây đang có sóng dừng xảy ra, dao động với phương trình u = acos(10πx).cos(5πt) cm, với a > 0, x tính bằng m và t tính bằng s. Hỏi điểm C cách M là 10/6 cm, đang dao động với biên độ là 6 cm thì giá trị a bằng bao nhiêu?

Hướng dẫn giải

Theo đề biên độ dao động là A_C = |acos(10πx)|

Từ đề bài cho:

• A_C = 6 cm.
• x = CM = 10/6 cm = 1/60 (m)

Thay số vào biểu thức biên độ: $6 = \left| {a.\cos \left( {10\pi .\frac{1}{{60}}} \right)} \right| \Leftrightarrow 6 = \left| {a.\cos \left( {\frac{\pi }{6}} \right)} \right| \Rightarrow a = 4\sqrt 3 \left( {cm} \right)$

Kết luận: \[a = 4\sqrt 3 \left( {cm} \right)\]

Ví dụ 3: Một điểm M trên dây có sóng dừng xảy ra đang dao động với phương trình u = 2sin(cx).cos(100πt – π/6), với x tính bằng m; t tính bằng s. Nếu biết tốc độ truyền sóng trên dây là 10 m/s thì giá trị c bằng bao nhiêu?

Hướng dẫn giải

theo đề bài:

• Phương trình sóng: u = 2sin(cx).cos(100πt – π/6)
• v = 10 m/s

Áp dụng công thức đã học ở trên: \[v = \frac{\omega }{{\frac{{2\pi }}{\lambda }}} \Rightarrow c = \frac{{2\pi }}{\lambda } = \frac{\omega }{v} = \frac{{100\pi }}{{10}} = 10\pi \]

Kết luận: c = 10π

Ví dụ 4: Trên một sợi dây có sóng dừng xảy ra, thấy một điểm gần nút nhất đang dao động với biên bằng biên độ tại nguồn sóng phát ra. Hỏi vị trị điểm N cách nút là bao nhiêu?

Hướng dẫn giải

Giả sử nguồn sóng dao động với phương trình u = bsin(ωt + α) cm thì biên độ dao động tại N là A_N = |b| nên

\[b = \left| {2b\sin \left( {\frac{{2\pi x}}{\lambda }} \right)} \right| \to \left| {\sin \left( {\frac{{2\pi x}}{\lambda }} \right)} \right| = \frac{1}{2}\]

Vì N gần nút nhất nên khoảng cách sẽ thỏa mãn là x_min = λ/12

Kết luận: N cách nút ngắn nhất là x_min = λ/12

Trên đây là mình đã giới thiệu với bạn những kiến thức trọng tâm về phương trình sóng dừng. Hy vọng với những chia sẻ quan trọng ở trên đã phần nào giúp bạn hiểu hơn về chủ đề nâng cao này.