Vị trí vân sáng và vân tối trong giao thoa ánh sáng

Dạng toán vị trí vân giao thoa là một chủ đề quan trọng thuộc chương giao thoa ánh sáng. Những năm gần đây chủ đề này thường nằm trong câu 7 đến 8 điểm.

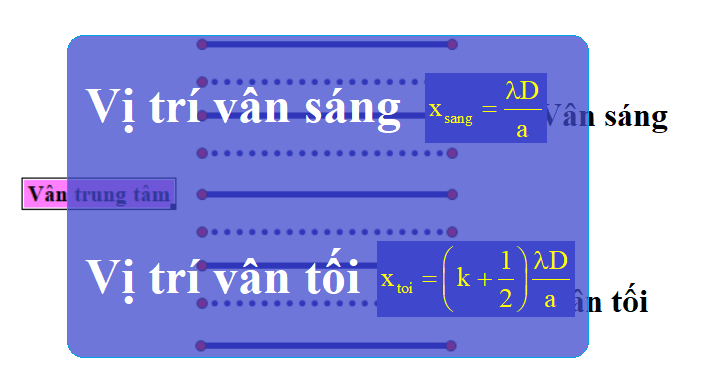
1. Vị trí vân sáng

Vị trí vân sáng trên màn được xác định theo công thức: $x = k\frac{{\lambda D}}{a}$

Ví dụ 1: Người ta làm một thí nghiệm giao thoa ánh sáng có a = 2 mm, D = 4 m. Hai nguồn sáng được chiếu bằng ánh sáng có bước sóng λ = 0,55μm. Hỏi vị trí vân sáng bậc 3 cách vân trung tâm là bao nhiêu?

Hướng dẫn giải

Theo đề bài:

• Hai khe cách nhau a = 2 mm = 2.10^-3 m
• Khoảng cách từ 2 khe tới màn D = 4 m
• Bước sóng λ = 0,55μm = 0,55.10^-6 m

Vị trí vân sáng bậc 3 ứng với k = 3 nên ta có: $\left| {{x_3}} \right| = k\frac{{\lambda D}}{a} = 3.\frac{{0,{{55.10}^{ – 6}}.4}}{{{{2.10}^{ – 3}}}} = 3,{3.10^{ – 3}}\left( m \right) = 3,3\left( {mm} \right)$

Kết luận: Vị trí vân sáng bậc 3 cách vân sáng chính giữa là 3,3 mm.

Ví dụ 2: Làm một thí nghiệm iang về giao thoa ánh sáng với dữ liệu ban đầu là S₁,S₂ = 1(mm), λ = 0,76 (µm) và D = 3m. Điểm A cách vân chính giữa 4,56mm là vân sáng thứ mấy?

Hướng dẫn giải

Theo đề bài:

• Khoảng cách giữa 2 khe a = 1(mm)
• Bước sóng ánh sáng λ = 0,76 (µm)
• Khoảng cách từ màn tới hai khe D = 3m

Theo đề, điểm A có tọa độ x_A = 4,56mm

Biên đổi công thức vị trí vân sáng: ${x_{sang}} = ki \to k = \frac{{{x_{sang}}}}{i} = \frac{{{x_{sang}}}}{{\frac{{\lambda D}}{a}}} = \frac{{4,{{56.10}^{ – 3}}}}{{2,{{28.10}^{ – 3}}}} = 2$

Kết luận: Tại điểm A là vân sáng bậc 2

2. Vị trí vân tối

Vị trí vân sáng trên màn được xác định theo công thức: $x = \left( {k + \frac{1}{2}} \right)\frac{{\lambda D}}{a}$

Ví dụ 2: Làm một thí nghiệm Y-ang về giao thoa ánh sáng, biết a = 1 mm, D = 1,3 m, λ = 0,61μm. Hỏi vị trí vân tối thứ 6 cách vân chính giữa là bao nhiêu?

Hướng dẫn giải

Theo đề:

• Hai khe cách nhau a = 1 mm = 1.10^-3 m
• Khoảng cách từ 2 khe tới màn D = 1,3 m
• Bước sóng λ = 0,61μm = 0,61.10^-6 m

Vị trí vân tối thứ 6 ứng với k = 5 nên: $\left| {{x_{t6}}} \right| = \left( {{k_6} + \frac{1}{2}} \right)\frac{{\lambda D}}{a} = \left( {5 + \frac{1}{2}} \right)\frac{{0,{{61.10}^{ – 6}}.1,3}}{{{{1.10}^{ – 3}}}} = 4,{3615.10^{ – 3}}\left( m \right) = 4,3615\left( {mm} \right)$

Kết luận: Kết luận vân tối thứ 6 cách vân chính giữa là 4,3615 (m)

Ví dụ 3: Làm thí nghiệm giao thoa ánh sáng biết S₁,S₂ = 1mm, λ = 0,5µm, D = 3m. Điểm M cách vân trung tâm 5,25 mm là vân gì?

Hướng dẫn giải

Theo đề bài:

• Khoảng cách giữa 2 khe là a = 1 mm = 10^-3 (m)
• Bước sóng λ = 0,5µm = 0,5.10^-6 (m)
• Khoảng cách từ 2 khe tới màn D = 3 m
• Vị trí M là x = 5,25 mm = 5,25.10^-3 m

Theo công thức ${x_{toi}} = \left( {{k_{toi}} + \frac{1}{2}} \right)i \to k = \frac{{{x_{toi}}}}{i} – \frac{1}{2} = 3$

Kết luận: Tại điểm M là vân tối thứ 2.

Ví dụ 3: Trên trường giao thoa sóng ánh sáng người ta thấy tại điểm M là vân tối thứ 3, người ta đo khoảng cách từ vân chính giữa tới M có độ dài là 4,8 mm. Khi đó vân sáng thứ 7 cách M là bao nhiêu?

Hướng dẫn giải

Theo đề:

• Tại điểm M là vân tối thứ 3 nên k = 2
• Vị trí x_M = 4,8 mm
• Vị trí vân sáng thứ 7 là x₇

Theo công thức đã được học ta biến đổi đại số một chút:

$\left. \begin{array}{l} {x_t} = \left( {{k_t} + 0,5} \right).i\\ {x_s} = {k_s}.i \end{array} \right\} \to \frac{{{x_s}}}{{{x_t}}} = \frac{{{k_s}}}{{{k_t} + 0,5}} \Rightarrow {x_s} = \frac{{{k_s}}}{{{k_t} + 0,5}}.{x_t}$

Thay số vào biểu thức trên: ${x_s} = \frac{7}{{2 + 0,5}}.4,8 = 13,44\left( {mm} \right)$

Vân sáng thứ 7 cách điểm M là: Δx = x₇ – x_M = 13,44 – 4,8 = 8,64(mm)

Kết luận: Vị trí vân sáng thứ 7 cách vân tối thứ 3 là 8,64 mm.

Qua bài viết này các bạn đã biết tìm được vị trí vân sáng cũng như vị trí vân tối nếu biết được a, D và λ. Tuy nhiên từ 2 công thức này có thể kết hợp với nhau sinh ra bài toán khá hay khiến học sinh cực hay nhầm, nhất là khi người gia đề chú tâm khai thác vào k. Nói vậy để bạn ôn cẩn thận không được chủ quan.